Throughout the evolution, several metrics have been introduced to evaluate the performance of a Machine Learning algorithm or model. Sometimes it can be tricky to choose the correct metric for evaluating our model. In this article I have tried to discuss some basic matrics used in ML-related tasks and when to use which metric.
Before jumping into the metrics directly, let’s explore a core concept — Confusion Matrix. It is not a metric, but it is important to know the concept as some metrics directly use these concepts.
Confusion Matrix
The confusion matrix is a performance measurement for a machine learning classification problem where output can be two or more classes. We can also call it Error Matrix. It allows the visualization of the performance of a model in a tabular form. Each row of the confusion matrix represents the instances of a predicted class. On the other hand, each column represents the instances of an actual class. The following figure shows a confusion matrix of a two-class classification problem.

With this figure, we are going to learn some new terminologies: True Positive (TP), False Positive (FP), False Negative (FN), and True Negative (TN).
True Positive (TP)
This predicted positive is actually or truly positive. This means the predicted class by a model is positive and the actual class is also positive. For example: let we are trying to identify the images of the tennis balls. For an image the model predicted it like a tennis ball and the ball in the image is actually a tennis ball. So this is a true positive.
False Positive (FP)
The model predicted an instance as positive and it is false. This means the predicted class is positive but the actual class is negative. For the previous scenario let the model predicted an image as a tennis ball but it is not a tennis ball.
False Negative (FN)
The model predicted an instance as negative and it is false. This means the predicted class is negative but the actual class is positive. For the same example, let the model predicted an image as not a tennis ball but it is actually a tennis ball.
True Negative (TN)
The model predicted an instance as negative and it is actually negative. Like the model predicted an image is not a tennis ball and it is actually not a tennis ball.
With the basic concepts of the confusion matrix, let’s now jump on the matrics we use in different ML tasks starting with the very common one — Accuracy.
Accuracy
Accuracy is the simplest and one of the most commonly used metrics. It is defined as the number of corrected predictions out of the total number of predictions. Very often we also express it into percentile. In this case, the accuracy score is multiplied by 100. So,
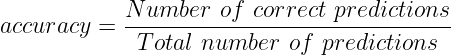
We can define accuracy using the confusion matrix also. Accuracy is the sum of total TPs and TNs divided by total data points or instances. So,
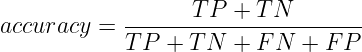
When to use Accuracy?
This metric — accuracy, can reflect a good result or understanding when the data is balanced i.e. each class contains about the same amount of data.
When not to use Accuracy?
Accuracy might not be a wise choice as a metric when there is an imbalance in the data. Let’s consider a scenario: for a binary classification (positive and negative) task we are working with a data set where 75% of total data belongs to the positive class. If each time no matter what, the model predicts a data instance to be positive, the model’s accuracy will be around 75%. This might be a good score but actually, the model is not good enough!
Precision
This metric indicates how many of the samples that are classified to be positive are actually positive. Precision attempts to answer the question: “What proportion of positive predictions was actually correct?”. We can define precision as:
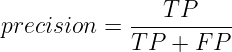
It is the ratio of true positives and all predictive positives (TP and FP). Thus precision is also called True Positive Accuracy.
When to use Precision?
Precision can be used when the false negative is of less concern. Let’s have a look at the following cases:
- Let’s assume you want to buy some good paintings but you don’t know much about painting; so you are using a machine learning model. You would buy a painting only if the model predicts it as a good painting. In this case, using precision is a good choice. Because you would buy a painting only if it is a good painting (correctly predicted true positive). It does not matter whether it is predicting a ‘good painting’ as a ‘not good painting’, as it is not costing you (you are not buying the painting). But predicting a ‘not good painting’ as a ‘good painting’ can result in a great cost to you (as you will buy it). Finally, it can be said, precision can be used when the cost of false positives is high or the cost of false negatives is low.
- In the case of YouTube recommendations, precision can be used. Because they want to show you the content you like (true positive) and it matters lesser if they miss any content you liked also (false negative with low cost). But recommending content that you do not like (false positive) can result in losing you as a client (high cost of false positive).
Recall
This metric, also known as Sensitivity, signifies to what extent all data points that needed to be classified as positive were classified as positive. It attempts to answer the question: “What proportion of actual positives was identified correctly?”. Recall can be defined as:
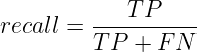
From the figure, we can see that Recall is the ratio of true positives and all actual positives (TP and FN). Recall aims to identify all True Positive cases. Recall also gives a measure of how accurately a model can identify the relevant data.
When to use Recall?
Recall can be used when the cost of false negative is high or false negative is of higher concern. Let’s have a look at the following cases:
- You have designed a model for predicting if a person is sick or not. In this case, using recall is a wise decision. Because if a person is sick but the model predicts him/her as not sick (false negative), the person can suffer in a critical situation or even death (high cost). On the other hand, if the model predicts a healthy person as sick (false positive), a recheck can be done (low cost). So, recall can be used when the cost of false negatives is high or the cost of false positives is low.
- Assume you are working for a product-selling website that gets a few thousand users per day. The company wants to call each possible buyer from using the user’s provided information. Your task is to design a model that can predict if a user is a possible buyer. In this case, to evaluate the performance of your model, you would like to use recall. Because not being able to predict a possible buyer (false negative) can reduce the sale of the company (high cost). It doesn’t matter if the model predicts a not possible buyer as a possible buyer (false positive). Because it won’t affect the sale (low cost). But not predicting a possible buyer can result in a huge loss.
The tradeoff and F1-score
Depending on the application we can choose either precision or recall. Unfortunately, precision and recall are often in tension. That is, improving precision typically reduces recall and vice versa (have a look here). This indicates if we want to increase recall or precision, another one has to be a tradeoff, thus the other score will reduce. But there can be situations where both of these metrics can be significant. Another metric known as F1-score can take into account both of these metrics. F1-score is the Harmonic mean of the Precision and Recall and defined as:
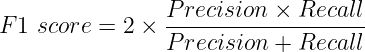
F1 score takes both false positives and false negatives into account, thus seeks a balance between these.
When to use F1-score?
This metric can be used when both Precision and Recall are significant and have almost the same cost. Let’s consider the following scenario:
Let a model checks someone’s health conditions and apply medications if necessary. In this case, using the F1-score is a good choice. Because failing to predict the right disease can be life-threatening (thus requiring high recall), predicting a wrong disease and applying medications can cause several side effects and complications (thus requiring high precision). In this case, the F1-score can be measured and take into account.
In this article, we have seen how the metrics can evaluate the models from different perspectives. More importantly, we have seen some scenarios where the metrics can be used to evaluate a model’s performance with more confidence.
This article is written as a learning process of mine. Any suggestions or opinions will be highly appreciated. Reach me through LinkedIn, Facebook, Email, or find me on GitHub.
References
Writing this article was a great journey for me. Throughout the time I have read several articles and learned a lot. These articles also helped me writing this post. I am truly grateful to the authors. The articles that empowered me are as following:
- 20 Popular Machine Learning Metrics. Part 1: Classification & Regression Evaluation Metrics by Shervin Minaee(link)
- Understanding Confusion Matrix by Sarang Narkhede (link)
- Classification: Precision and Recall (link)
- When is precision more important over recall? asked question on StackExchange by Rajat (link)